Fractions

What do we know about fractions?

 

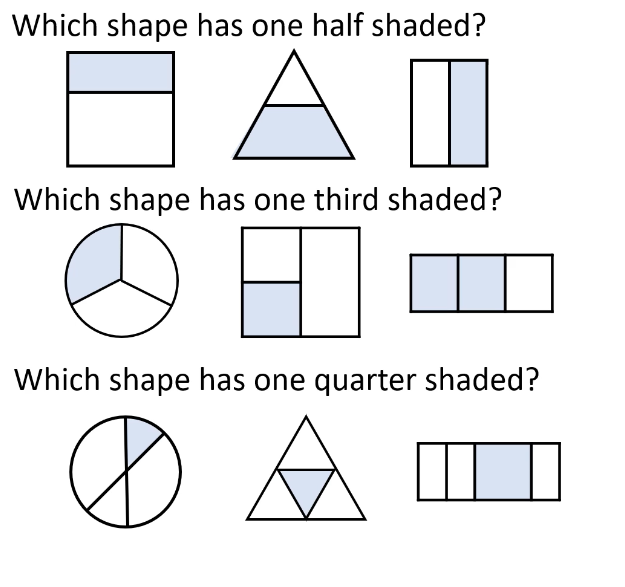
LO: To identify 1/3, 1/4, 1/2, 2/4, 3/4 and demonstrate that all parts must be equal parts of the whole.

LO: To accurately place fractions and decimals on a number line.  

LO: To recall and solve problems using equivalences between simple fractions,

LO: To convert improper fractions to mixed numbers and vice versa. 

LO: To use and interpret different representations of fractions, e.g. mixed numbers and improper fractions. 

When we write a fraction, we often write three parts. The Numerator, the Fraction bar and the Denominator.

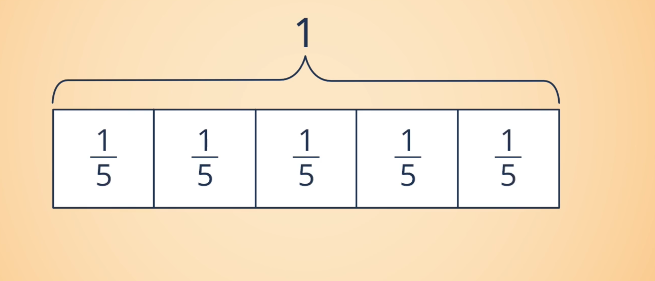
If I were to take a bar of chocolate, I could split that bar into five equal parts. These would be called fifths. Parts of a fraction are usually equal, and when pieced back together, they make a whole piece again. 

We can also do this with a packet of sweets. If I open a packet of sweets and share them out equally I could create a fraction of my whole packet.

For example, if I had 18 sweets, 1/2 of my packet would equal 9, or I could split my packet into 1/18.

 

Let's try!

 

Rules!

Do not eat your sweets until the end of the lesson.

Do not touch anyone else's sweets.

Have fun!

 

If your sweets represent a whole, how could you show part of the whole?

 

Let's make fractions!

Using the language Numerator and Denominator, what fractions could I make using my sweets?

 

Could I make fractions based on the colour of my Skittles?

 

Let's write down as many fractions as you can.

 

Could I add two colours together to find out the total fraction of those colours?

 

 

Comparing fractions

Discuss in pairs 

• Which colour takes up the largest fraction?

• Which is the smallest?

• Are any colours equal?

• Create a number line with the smallest fraction to the biggest

 

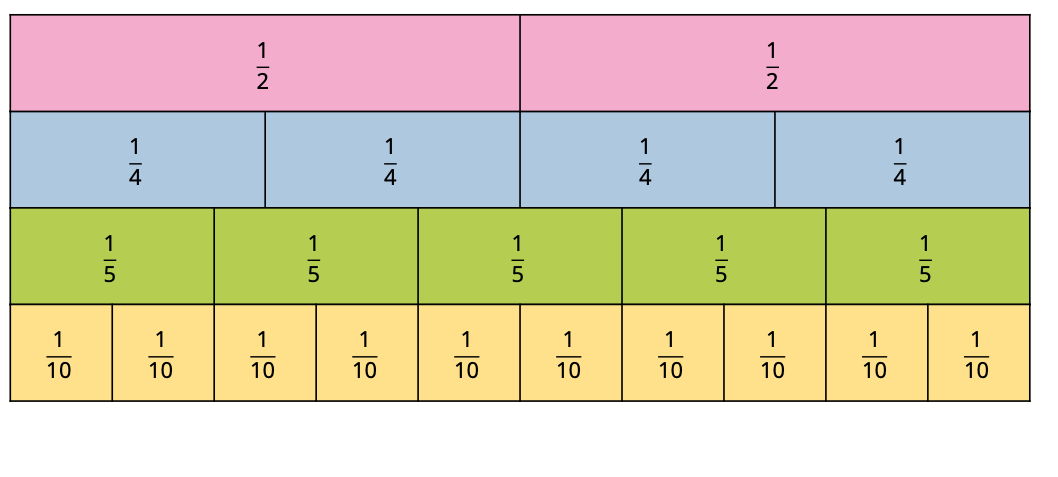
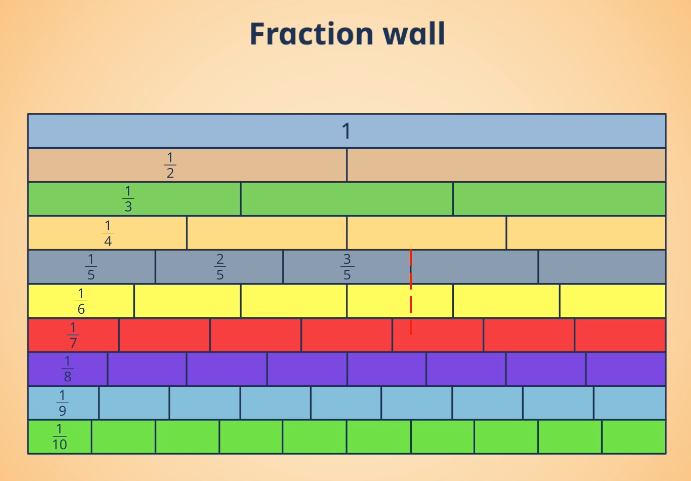
A Fraction Wall can help us find equivalent fractions. For example, 1/2 is the same as 5/10. Why is that? 

What other fractions are equivalent?

Fraction Wall

 

Convert Fractions to Simplest Form

Using your Skittles fractions, can you simplify each fraction?

Example:

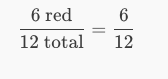
• “Can you divide the numerator and denominator by the same number?”

• “What is the simplest form of your fraction?”